Content
更好的效果PDF:pdf文章列表 | Asiv’s Blog (niceasiv.cn)
Factoring challenge #1:
Your goal in this project is to break RSA when the public modulus $N$ is generated incorrectly. This should serve as yet another reminder not to implement crypto primitives yourself.
Normally, the primes that comprise an RSA modulus are generated independently of one another. But suppose a developer decides to generate the first prime $p$ by choosing a random number $R$ and scanning for a prime close by. The second prime $q$ is generated by scanning for some other random prime also close to $R$. We show that the resulting RSA modulus $N=p q$ can be easily factored.
在公开的N没有被正确的生成时破解RSA。通常在RSA中构成模数N的素数q和p,应该独立生成。如果开发者使用一个随机数R,并选择R附近的两个素数作为q和p,那么这种情况情况下生成的RSA模数N就很容易被破解。
Suppose you are given a composite(合数) $N$ and are told that $N$ is a product of two relatively close primes $p$ and $q$, namely $p$ and $q$ satisfy $$ |p-q|<2 N^{1 / 4} $$ Your goal is to factor $N$. Let $A$ be the arithmetic(算数) average of the two primes, that is $A=\frac{p+q}{2}$. Since $p$ and $q$ are odd(奇数), we know that $p+q$ is even and therefore $A$ is an integer(整数).
可以得到 $A=\frac{p+q}{2}<N^{\frac{1}{4}}$
To factor $N$ you first observe that under condition $\left.{ }^\right)$ the quantity $\sqrt{N}$ is very close to $A$. In particular, we show below that: $$ {A-\sqrt{N}<1} $$ But since $A$ is an integer, rounding $\sqrt{N}$ up to the closest integer reveals the value of $A$. In code, $A=$ ceil $(\operatorname{sqrt}(N))$ where “ceil” is the ceiling function. Visually, the numbers $p, q, \sqrt{N}$ and $A$ are ordered as follows:
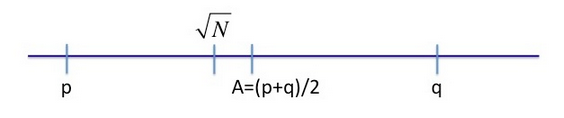
Since $A$ is the exact mid-point between $p$ and $q$ there is an integer $x$ such that $p=A-x$ and $q=A+x$. But then $N=p q=(A-x)(A+x)=A^2-x^2$ and therefore $x=\sqrt{A^2-N}$.
Now, given $x$ and $A$ you can find the factors $p$ and $q$ of $N$ since $p=A-x$ and $q=A+x$. You have now factored $N$ !
因为$A$是$p$,$q$的中点
$\therefore$ $p=A-x$ $q=A+x$$\implies N=p q=(A-x)(A+x)=A^2-x^2$
$\therefore x=\sqrt{A^2-N}$
所以得到$x$的值可以得到$p,q$的取值
Further reading: the method described above is a greatly simplified version of a much more general result on factoring when the high order bits of the prime factor are known.
In the following challenges, you will factor the given moduli using the method outlined above. To solve this assignment it is best to use an environment that supports multi-precision arithmetic and square roots. In Python you could use the gmpy2 module. In C you can use GMP.
The following modulus $N$ is a products of two primes $p$ and $q$ where $|p-q|<2 N^{1 / 4}*$. Find the smaller of the two factors and enter it as a decimal integer in the box below.
N = 17976931348623159077293051907890247336179769789423065727343008115 \
77326758055056206869853794492129829595855013875371640157101398586 \
47833778606925583497541085196591615128057575940752635007475935288 \
71082364994994077189561705436114947486504671101510156394068052754 \
0071584560878577663743040086340742855278549092581
For completeness, let us see why $A-\sqrt{N}<1$. This follows from the following simple calculation. First observe that $A^2-N=\left(\frac{p+q}{2}\right)^2-N=\frac{p^2+2 N+q^2}{4}-N=\frac{p^2-2 N+q^2}{4}=(p-q)^2 / 4$. Now, since for all $x, y: \quad(x-y)(x+y)=x^2-y^2$ we obtain $A-\sqrt{N}=(A-\sqrt{N}) \frac{A+\sqrt{N}}{A+\sqrt{N}}=$ $\frac{A^2-N}{A+\sqrt{N}}=\frac{(p-q)^2 / 4}{A+\sqrt{N}}$ Since $\sqrt{N} \leq A$ it follows that $A-\sqrt{N} \leq \frac{(p-q)^2 / 4}{2 \sqrt{N}}=\frac{(p-q)^2}{8 \sqrt{N}}$. By assumption (*) we know that $(p-q)^2<4 \sqrt{N}$ and therefore $A-\sqrt{N} \leq \frac{4 \sqrt{N}}{8 \sqrt{N}}=1 / 2$ as required.
$0<A-\sqrt{N}<1$$\implies A<\sqrt{N}+1$
$\text{proof:}$
${A}=\frac{p+q}{2}, {~N}={pq}$ $A$为整数
对左边:
$0<{A}-\sqrt{N}$ : 由基本不等式 $\sqrt{ab}\leq\frac{a+b}{2}$ 可以得到 $\sqrt{pq}<\frac{p+q}{2}$ 因为 $p\neq q$ ,所以无法取到等号,所以 $\sqrt{pq}<{A}$$\implies 0<A-\sqrt{N}$$\implies\sqrt{N}<{A}$
对右边:
$A-\sqrt{N}<1$,有:
$$ \mathrm{A}^2-\mathrm{N}=\left(\frac{\mathrm{p}+\mathrm{q}}{2}\right)^2-\mathrm{N}=\frac{\mathrm{p}^2+2 \mathrm{~N}+\mathrm{q}^2}{4}-\mathrm{N}=\frac{\mathrm{p}^2-2 \mathrm{~N}+\mathrm{q}^2}{4}=\frac{(\mathrm{p}-\mathrm{q})^2}{4}\tag{1} $$ 对于 $A-\sqrt{N}$ ,有: $$ A-\sqrt{N}=\frac{(A-\sqrt{N})(A+\sqrt{N})}{A+\sqrt{N}}=\frac{A^2-N}{A+\sqrt{N}}={A+\sqrt{N}}=\frac{\frac{(p-q)^2}{4}}{A+\sqrt{N}} \tag{1} $$ 由于 $\sqrt{N}<A$ ,那么, $$ A-\sqrt{\mathrm{N}}=\frac{\frac{(\mathrm{p}-\mathrm{q})^2}4}{\mathrm{~A}+\sqrt{\mathrm{N}}}<\frac{\frac{(\mathrm{p}-\mathrm{q})^2}4}{\sqrt{\mathrm{N}}+\sqrt{\mathrm{N}}}=\frac{(\mathrm{p}-\mathrm{q})^2}{8 \sqrt{\mathrm{N}}} \tag{3} $$ 由于challenge #1满足 $|p-q|<2 N^{1 / 4}$ ,即 $(p-q)^2<4 \sqrt{N}$ ,最后得到: $$ \mathrm{A}-\sqrt{\mathrm{N}}=\frac{(\mathrm{p}-\mathrm{q})^2}{8 \sqrt{\mathrm{N}}}<\frac{4 \sqrt{\mathrm{N}}}{8 \sqrt{\mathrm{N}}}=1 / 2<1 \tag{4} $$
Enter the answer for factoring challenge #1 in the box below:
13407807929942597099574024998205846127479365820592393377723561443721764030073662768891111614362326998675040546094339320838419523375986027530441562135724301
code:
import gmpy2
def task1():
#初始化大整数n
n =gmpy2.mpz('17976931348623159077293051907890247336179769789423065727343008115' +
'77326758055056206869853794492129829595855013875371640157101398586' +
'47833778606925583497541085196591615128057575940752635007475935288' +
'71082364994994077189561705436114947486504671101510156394068052754' +
'0071584560878577663743040086340742855278549092581')
#得到n的平方根的整数部分
A,r=gmpy2.isqrt_rem(n)#A为整数部分,r为余数
if r>0:
A+=1
#得到x
x=gmpy2.isqrt(A**2-n)
#得到p和q
p,q=A-x,A+x
#检验p和q是否为素数且p*q=n
if gmpy2.is_prime(p) and gmpy2.is_prime(q) and gmpy2.mul(p,q)==n:
print('p=',p)
print('q=',q)
if __name__ == '__main__':
task1()
Factoring challenge #2:
The following modulus $N$ is a products of two primes $p$ and $q$ where $|p-q|<2^{11} N^{1 / 4}$. Find the smaller of the two factors and enter it as a decimal integer.
Hint: in this case $A-\sqrt{N}<2^{20}$ so try scanning for $A$ from $\sqrt{N}$ upwards, until you succeed in factoring $N$.
$\text{Proof:}$
由Factoring challenge #1的证明
${A}=\frac{p+q}{2}, {~N}={pq}$ $A$为整数
$|p-q|<2^{11} N^{1 / 4}$$\implies$$(p-q)^2<2^{22}\sqrt{N}$
由公式$3$可以得到 $$ 0<A-\sqrt{\mathrm{N}}=\frac{\frac{(\mathrm{p}-\mathrm{q})^2}4}{\mathrm{~A}+\sqrt{\mathrm{N}}}<\frac{\frac{(\mathrm{p}-\mathrm{q})^2}4}{\sqrt{\mathrm{N}}+\sqrt{\mathrm{N}}}=\frac{(\mathrm{p}-\mathrm{q})^2}{8 \sqrt{\mathrm{N}}}<\frac{2^{22}\sqrt{N}}{8\sqrt{N}}=2^{19}\tag{5} $$ 因此$A$的范围应该在$(\sqrt{N},2^{19}+\sqrt{N})$
N =6484558428080716696628242653467722787263437207069762630604390703787 \
9730861808111646271401527606141756919558732184025452065542490671989 \
2428844841839353281972988531310511738648965962582821502504990264452 \
1008852816733037111422964210278402893076574586452336833570778346897 \
15838646088239640236866252211790085787877
Enter the answer for factoring challenge #2 in the box below:
25464796146996183438008816563973942229341454268524157846328581927885777969985222835143851073249573454107384461557193173304497244814071505790566593206419759
Code
import gmpy2
def task2():
#初始化大整数n
n =gmpy2.mpz('6484558428080716696628242653467722787263437207069762630604390703787'+'9730861808111646271401527606141756919558732184025452065542490671989'+
'2428844841839353281972988531310511738648965962582821502504990264452'+'1008852816733037111422964210278402893076574586452336833570778346897 '+'15838646088239640236866252211790085787877')
#初始化得到n的平方根的整数部分
A=gmpy2.isqrt(n)+1#A为整数部分 向上取整A^2>n
#循环次数
max_count=pow(2,20)
#得到x
for i in range(max_count):
x,r=gmpy2.isqrt_rem(A**2-n)
#得到p和q
if r==0:
p,q=A-x,A+x
#检验p和q是否为素数且p*q=n
if gmpy2.is_prime(p) and gmpy2.is_prime(q) and gmpy2.mul(p,q)==n:
print('[!] Found it count=',i)
print('p=',p)
print('q=',q)
break
A+=1
if __name__ == '__main__':
task2()
Factoring challenge #3:
The following modulus $N$ is a product of two primes $p$ and $q$ where $|3 p-2 q|<N^{1 / 4}$. Find the smaller of the two factors and enter it as a decimal integer. Hint: first show that $\sqrt{6 N}$ is close to $\frac{3 p+2 q}{2}$ and then adapt the method in challenge #1 to factor $N$.
N =72006226374735042527956443552558373833808445147399984182665305798191 \
63556901883377904234086641876639384851752649940178970835240791356868 \
77441155132015188279331812309091996246361896836573643119174094961348 \
52463970788523879939683923036467667022162701835329944324119217381272 \
9276147530748597302192751375739387929
$A-\sqrt{6N}<\frac{1}{8\sqrt{6}}$
$\text{Proof:}$
定义$A=\frac{3p+2q}{2}$即$A$是$3p$和$2q$的中点,且$3p$是奇数,$2q$是偶数,所以$A$一定不是整数
由challenge #1同理
$\because $$\text{A是3p,2q的中点}$
$\therefore$ $p=\frac{A-x}{3}$ $q=\frac{A+x}{2}$$\implies N=p q=\frac{(A-x)(A+x)}{6}=\frac{A^2-x^2}{6}$(这里其实$\frac{A-x}{3}$有可能为p或者q,还要根据$A-x$是否被3除尽就可确定)
$\therefore x=\sqrt{A^2-6N}$
所以得到$x$的值可以得到$p,q$的取值
由$\sqrt{ab}<=\frac{a+b}{2}$
$\therefore{\sqrt{6pq}<\frac{3p+2q}{2}}$$\implies \sqrt{6N}<A$
$$ A-\sqrt{6N}=\frac{A^2-6N}{A+\sqrt{6N}}=\frac{\frac{(3p-2q)^2}{4}}{A+\sqrt{6N}}<\frac{\frac{(3p-2q)^2}{4}}{\sqrt{6N}+\sqrt{6N}}=\frac{\frac{(3p-2q)^2}{4}}{2\sqrt{6N}} \tag {6} $$ 由于challenge3满足$|3 p-2 q|<N^{1 / 4}$即是$(3p-2q)^2<\sqrt{N}$ $$ A-\sqrt{6N}<\frac{\frac{(3p-2q)^2}{4}}{2\sqrt{6N}}<\frac{1}{8\sqrt{6}} $$
Enter the answer for factoring challenge #3 in the box below:
21909849592475533092273988531583955898982176093344929030099423584127212078126150044721102570957812665127475051465088833555993294644190955293613411658629209
code
from decimal import Decimal, getcontext
def isqrt(n):
x = n
y = (x + 1) // 2
while y < x:
x = y
y = (x + n // x) // 2
return x
def task3():
n=720062263747350425279564435525583738338084451473999841826653057981916355690188337790423408664187663938485175264994017897083524079135686877441155132015188279331812309091996246361896836573643119174094961348524639707885238799396839230364676670221627018353299443241192173812729276147530748597302192751375739387929
getcontext().prec=350#设置精度
A=Decimal(isqrt(6*n))+Decimal(0.5)
while True:
x=Decimal(A**2-6*Decimal(n)).sqrt()
p=int(A-x)
q=int(A+x)
if p*q==6*n:
if p%3==0 and q%2==0:
p//=3
q//=2
break
if p%2==0 and q%3==0:
p//=2
q//=3
break
A+=1
print(p)
print(q)
if __name__ == '__main__':
task3()
4.
The challenge ciphertext provided below is the result of encrypting a short secret ASCII plaintext using the RSA modulus given in the first factorization challenge.
The encryption exponent used is $e=65537$ The ASCII plaintext was encoded using PKCS v1.5 before the RSA function was applied, as described in PKCS.
Use the factorization you obtained for this RSA modulus to decrypt this challenge ciphertext and enter the resulting English plaintext in the box below. Recall that the factorization of $N$ enables you to compute $\varphi(N)$from which you can obtain the RSA decryption exponent.
Challenge ciphertext (as a decimal integer):
22096451867410381776306561134883418017410069787892831071731839143676135600120538004282329650473509424343946219751512256465839967942889460764542040581564748988013734864120452325229320176487916666402997509188729971690526083222067771600019329260870009579993724077458967773697817571267229951148662959627934791540
After you use the decryption exponent to decrypt the challenge ciphertext you will obtain a PKCS1 encoded plaintext.To undo the encoding it is best to write the decrypted value in hex.You will observe that the number starts with a ‘0x02’ followed by many random non-zero digits.Look for the ‘0x00’ separator and the digits following this separator are the ASCII letters of the plaintext.
(note: the separator used here is ‘0x00’, not ‘0xFF’ as stated in the lecture)
公钥就是 N,e 而 私钥就是N,d 加密 m^e ≡ c (mod n) 解密 c^d ≡ m (mod n)
import binascii
import gmpy2
def task4():
c = gmpy2.mpz('22096451867410381776306561134883418017410069787892831071731839143676135600120538004282329650473509424343946219751512256' +
'46583996794288946076454204058156474898801373486412045232522932017648791666640299750918872997169052608322206777160001932' +
'9260870009579993724077458967773697817571267229951148662959627934791540')
n = gmpy2.mpz('17976931348623159077293051907890247336179769789423065727343008115' +
'77326758055056206869853794492129829595855013875371640157101398586' +
'47833778606925583497541085196591615128057575940752635007475935288' +
'71082364994994077189561705436114947486504671101510156394068052754' +
'0071584560878577663743040086340742855278549092581')
e =gmpy2.mpz(65537)
a = gmpy2.isqrt(n) + 1
x = gmpy2.isqrt(a**2 - n)
p = a - x
q = a + x
fi = (p-1) * (q-1)#欧拉函数
d = gmpy2.invert(e, fi)#求e的模fi的逆元
r = gmpy2.powmod(c, d, n)#求c的d次方模n
#PKCS解密
m = gmpy2.digits(r, 16).split('00')[1]#将r转换为16进制,然后以00为分隔符分割,取第二个元素
return binascii.unhexlify(m.encode('utf-8'))
if __name__ == '__main__':
print(task4())
Factoring lets us break RSA.